[CS][알고리즘] 정렬 알고리즘

퀵 정렬 (Quick Sort)

• 임의의 Pivot 을 두고 Pivot의 왼쪽에는 Pivot보다 작은 값을, 오른쪽에는 큰 값을 두는 과정을 반복하는 알고리즘

분할

• 배열의 분할 : 배열로부터 임의의 수(Pivot; 피벗)을 가져와 피벗보다 작은 모든 수는 피벗의 왼쪽에, 피벗보다 큰 모든 수는 피벗의 오른쪽에 두는것

• 알고리즘

  1. 임의의 값을 피벗으로 정한다.
  2. 피벗을 제외한 맨 왼쪽의 수를 lp, 피벗을 제외한 맨 오른쪽의 수를 rp라고 하자.
  3. lp를 한 셀씩 계속 오른쪽으로 옮기면서 피벗보다 크거나 같은 값에 도달하면 멈춘다.
  4. rp를 한 셀씩 계속 왼쪽으로 옮기면서 피벗보다 작거나 같은 값에 도달하면 멈춘다.
  5. lp와 rp의 값을 교환한다.
  6. 두 값이 같거나 lp가 rp 바로 오른쪽으로 이동할 때까지 3~5를 반복한다.
  7. rp가 현재 가리키고 있는 값과 피벗을 비교한 후 교환한다.
  

1. 54를 피벗으로 정한다.

2. 피벗을 제외한 맨 왼쪽의 수 lp=26, 맨 오른쪽의 수 rp=20
3. lp가 54보다 크거나 같은값인 93에 도달했으므로 lp=93
4. rp가 54보다 작거나 같은값인 20에 도달했으므로 rp=20
5. lp와 rp의 값 교환 » lp=20, rp=93

1. 1. lp가 피벗보다 크거나 같은값인 77에 도달했으므로 lp=77

   2. rp가 피벗보다 작거나 같은값인 44에 도달했으므로 rp=44
   3. lp와 rp의 값 교환 » lp=44, rp=77

1. 1. lp가 피벗보다 크거나 같은값인 77에 도달했으므로 lp=77

   2. rp가 피벗보다 작거나 같은값인 31에 도달했으므로 rp=31
   3. lp가 rp의 바로 오른쪽으로 이동하였으므로 반복 종료

1. rp와 피벗 비교 후 교환 » {34, 26, 20, 17, 44, 31, 77, 55, 93}

2. 피벗이었던 54를 기준으로 54보다 작은 값은 왼쪽으로, 54보다 큰 값은 오른쪽으로 이동하였고, 피벗이 올바른 위치에 있게 되었다.

퀵 정렬

• 퀵 정렬은 분할로 시작한다.
• 알고리즘 ```
  1. 배열을 분할하여 피벗을 올바른 위치에 둔다.
  2. 피벗의 왼쪽과 오른쪽에 있는 하위 배열을 각각 또 다른 배열로 보고 분할을 반복한다.

즉, 각 하위 배열을 분할하고 각 하위 배열에 있는 피벗을 통해 더 작아진 하위 배열을 얻는다.

1. 하위 배열이 없을(0개 또는 1개) 때 까지 분할하는 과정을 반복한다. ```

퀵 정렬의 수행 시간 (복잡도)

• 최적 수행 시간 O(nlog₂n)
• 평균 수행 시간 O(nlog₂n)
• 최악 수행 시간 O(n²)

병합 정렬 (Merge Sort)

• 전체 원소를 하나의 단위로 분할한 후, 분할한 원소를 다시 병합해서 정렬하는 알고리즘

  

병합 정렬의 수행 시간 (복잡도)

• 최적 수행 시간 O(nlog₂n)
• 평균 수행 시간 O(nlog₂n)
• 최악 수행 시간 O(nlog₂n)

힙 정렬 (Heap Sort)

• 정렬할 입력 레코드들로 힙을 구성하고, 가장 큰 키값을 갖는 루트 노드를 제거하는 과정을 반복하여 정렬하는 알고리즘
• 완전 이진 트리 균형잡힌 이진 트리 로 입력 자료의 레코드를 구성

힙 (Heap)

• 힙 정렬을 위해 정해진 데이터를 힙 구조를 가지도록 만들어야 함
• 최솟값이나 최댓값을 빠르게 찾아내기 위해 완전 이진 트리를 기반으로 하는 트리
• 최대 힙 : 부모 노드 > 자식 노드 , 오름차순
• 최소 힙 : 부모 노드 < 자식노드 , 내림차순
• 트리 안에서 특정 노드 때문에 최대 힙이 붕괴되는 경우 힙 정렬 수행

힙 생성 알고리즘

• 힙 정렬을 위해 힙 생성 알고리즘을 사용
• 힙 생성 알고리즘 : 특정 하나의 노드를 제외하고는 최대 힙이 구성되어 있는 상태라고 가정을 하고, 특정한 ‘하나의 노드’에 대해서만 정렬을 수행하는 것

• 특정한 노드의 두 자식 중에서 더 큰 자식과 자신의 위치를 바꾸는 알고리즘

  

힙 정렬의 수행 시간 (복잡도)

• 최적 수행 시간 O(nlog₂n)
• 평균 수행 시간 O(nlog₂n)
• 최악 수행 시간 O(nlog₂n)

버블 정렬 (Bubble Sort)

• 인접한 두 개의 레코드 키값을 비교하여 크기에 따라 레코드 위치를 서로 교환하는 알고리즘

• 한 PASS를 수행할 때마다 가장 큰 값이 맨 뒤로 이동하기 때문에, 요소의 개수-1 번 PASS 수행하면 모든 숫자가 정렬

  

복잡도

• O(n²) : 제곱형 주요 처리 루프 구조가 2중인 경우, n크기가 작을 때에는 n²이 nlog₂n보다 빠를 수 있음

삽입 정렬 (Insertion Sort)

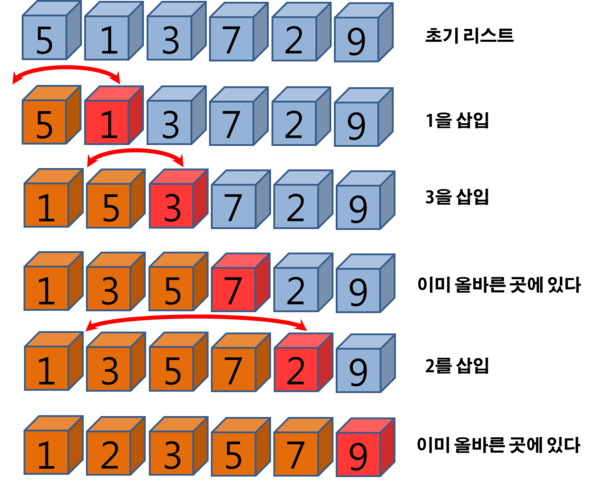
• n번째 키와 앞 (n-1)개 키를 비교하여 알맞은 순서에 삽입하는 알고리즘

• 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성

  

복잡도

• O(n²) : 제곱형 주요 처리 루프 구조가 2중인 경우, n크기가 작을 때에는 n²이 nlog₂n보다 빠를 수 있음

선택 정렬 (Selection Sort)

• 정렬되지 않은 데이터들에 대해 가장 작은 데이터를 찾아 정렬 되지 않은 부분의 가장 앞의 데이터와 교환하는 알고리즘

  

복잡도

• O(n²) : 제곱형 주요 처리 루프 구조가 2중인 경우, n크기가 작을 때에는 n²이 nlog₂n보다 빠를 수 있음